back

top

Home Code About Contact

n - ellipses

[7/12/23 ]  Formulating the problem of finding the largest convex subset (in a way that can be computed) is difficult in general, and I think that limiting the subsets to a certain shape could make things easier.

$n$-ellipses, ellipses with $n$ focal points, are always convex, and versatile as $n$ varies.

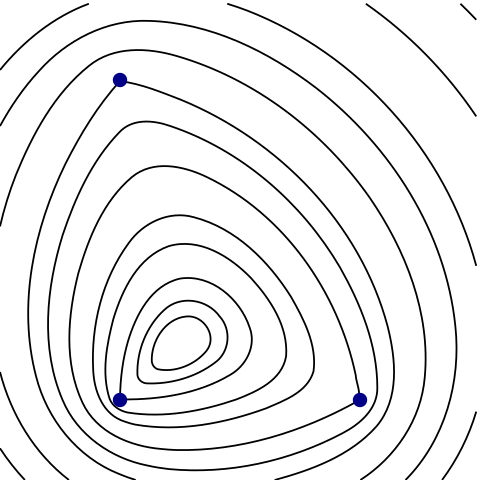
The resources I intend to use are:

1. Semidefinite Representations of The K-Ellipse – Nie, Parillo, and Sturmfels
2. The Geometry of Semidefinite Programming – Sturmfels
3. On the Approximation of Convex, Closed Plane Curves by Multifocal Ellipses – Erdös, Vincze
4. n-Ellipses and the Minimum Distance Sum Problem – Sekino

The item by Erdös is exactly what I’m looking for and it suggests that $n$-ellipses might be able to approximate any convex, closed plane curve.